AMEMA

• A lemniszkáta hat definícióját írom ide, az első egy mechanikus rajzológép elvét adja meg, a körző ismert dolog, ennek két fix pontja van és egy csuklós négyoldallal dolgozik, a második pedig egyszerűen csak arra gondol: a fókuszpontoktól vett távolságszorzat állandó.

1. ABCD négyszög CD oldalának felezőpontja megrajzolja, ha pl. AB=CD= √2 és AD=BC=1
2. A P pont megrajzolja, midőn pl. az F ( -√2 /2 , 0 ) és a G ( √2 /2 , 0 ) fókusz pontoktól vett PF * PG = 1/2 távolság szorzat állandó
3. az egyenlőoldalú hiperbola origó körüli körre vett inverz képe (az inverzió témáját később kidolgozom, most az a fontos egyelőre, hogy két másodrendű görbe hozza létre a negyedrendű görbét, lásd a B. pontot)
4. az egyenlőoldalú hiperbola érintőire origóból vont merőleges egyenesek talppontjai is megrajzolják (1-4. definíciók a fazekas.hu-n is megtalálhatóak)
5. annak a körseregnek a burkolója, amely körök középpontja a hiperbolára és egyúttal a hiperbola középpontja a körre illeszkedik
6. a tórusz érintősíkja kimetszi a tóruszból, melynek belső sugara és a generáló kör sugara egyenlőek (lásd még: The Lemniscate of Bernoulli, without Formulas – Arseniy V. Akopyan)

• A) A lemniszkáta két fókuszpontját nevezhetjük az alakzat két központjának, és akkor a görbe önmetszési pontját csomópontnak vagy kettőspontnak.
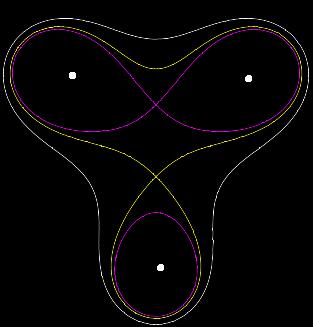
• B) Az 1. definíció egy mechanikus rajzológép általi szerkesztést tesz lehetővé – nem a jól ismert körzővel, hanem egy merev oldalakból álló csukló négyoldallal, amelynek nem egy fix pontja van, mint a körzőnek, hanem két fix pontja van. Ha ezt végiggondoljuk, és hozzávesszük a 2. definíciót, akkor még azt is elgondolhatjuk, hogy egy három fókuszó (három fix pontú) lemniszkáta három két fókuszó lemniszkáta egymásra hatásából jönne létre. Ekkor az ilyen görbe pontjának a három fókusz ponttól vett távolság szorzata lesz állandó. A kör és a hiperbola másodrendű görbe, a lemniszkáta negyedrendű görbe, utóbbi pedig hatodrendű lesz. Az egyenes elsőrendű, mert más egyenes vele egy metszéspontot ad, a kör és a kúpszelet max két metszéspontot ad egy egyenessel, a lemniszkáta azonban már negyedrendű görbe. – A hármas tagozódással foglalkozó antropozófusok számára a lemniszkáta és a tórusz kapcsolata fontos lehet, így talán a három fókuszó síkbeli lemniszkáta is érdekes képet ad.
  
• C) Hogyan lehet a térbe kihozni a síkbeli lemniszkátát? A síkbeli vonal helyett vegyünk egy szalagot, melyet ha összeragasztunk, akkor egy elég unalmas egyszerű karkötő-félét kapunk, egy hengerpalástot. Azonban, ha megcsavarjuk és összeragasztjuk, Möbiusz-szalagot kapunk, amelynek síknézete közel áll a lemniszkáta alakhoz. Ha a szabadságot és a szeretetet egymához képest olyannak látjuk, mint ami egy dolog két oldala, de nem választhatóak el egymástól mégse, akkor a térbeli Möbiusz-szalag jól mutatja, miről van szó. Ha elindulok a szabadság útján, akkor a szeretethez jutok el, és ha a szeretet útján haladok, akkor a szabadsághoz jutok el. Ezt a kettős képet még más valamihez is el lehet vinni. Ez pedig az évkör, amint a 12 szent éjszakán visszanézünk az elmúlt évre, egyszer, mint szabadság-, egyszer mint szeretet-áramlat szerint. Egy lapra ugyanis felírhatjuk az elmúlt év januárjához tartozó decembert, és utána a februárhoz tartozó novembert, de végül egy Möbiusz-szalagot kapunk, amit a síkon egy lemniszkátán végigfutó két fonál jelez. Csak az egyik fonalat a jövőből a másikat a múltból kell húzni. A múltból fejlődik ki a jövő felé a szabadság (január 6-tól előrehaladóan a gondolat) és a jövőből a múlt felé halad a szeretet (december 24-tól visszafelé haladóan az akarat). A két áramlat közt van a tudatunk, amely Möbiusz-szerűen egyszer a szabadság felé fordul, másszor a szeretet felé. Ezt úgy lehetne jól megfogalmazni, hogy a szabadság és a szeretet egymás inverz képe, egy átfordulás, vagy csavar kell hozzá.A fej és a végtagok is így fordulnak át egymásba, például a lélek útja során halál és az újraszületés között.
• D) Amikor a vonal önmagába visszatér, de a kiindulás és a visszatérés közt megfordul, az a lemniszkáta-forma. Ennek síkba vitelét kapjuk, ha a vonal helyett szalagot alkalmazunk, ez lesz a Möbiusz-szalag. Ha pedig olyan térbeli alakzatot keresünk, amelyik önmagába visszafordul, az a Klein-kancsó.